• A. Sequence with Digits
• B. Young Explorers
• C. Count Triangles
• D. Game With Array
• E. Restorer Distance

https://codeforces.com/contest/1355 (opens new window)

打一半和室友开黑去了哈哈哈哈哈哈反正不计分（不要学我）。

A. Sequence with Digits

这题我会证！首先对于百位来说，不可能从 x 跳到 x+2，只能从 x 变成 x+1 或者不变（因为最大变化量为 $9\times9=81$）。

这样的话大约 1000 次内，百位不可避免地从 9 变成 0，这样 min 的值是 0，变化量 min*max 就是一直是 0 了。

#include <bits/stdc++.h>
using namespace std;
#define repeat(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define repeat_back(i,a,b) for(int i=(b)-1,_=(a);i>=_;i--)
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
const int N=200010; typedef long long ll;
#define int ll
int a,k;
string s;
signed main(){
    int T; cin>>T;
    while(T--){
        cin>>a>>k;
        while(--k){
            s=to_string(a);
            int x=*min_element(s.begin(),s.end())-48;
            int y=*max_element(s.begin(),s.end())-48;
            if(x==0)break;
            a+=x*y;
        }
        cout<<a<<endl;
    }
    return 0;
}

B. Young Explorers

比赛中我自始至终都以为所有探险者都要组队，然后 emmm...

贪心，尽量组规模小的队，所以排个序就好了。

感谢 zkx 巨佬提供的代码（没错，我懒了补题）。

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+7;

int n;
int a[N];

inline void solve() {
  cin >> n;
  for (int i = 1; i <= n; ++i) {
    cin >> a[i];
  }
  sort(a+1, a+n+1);
  int res = 0;
  for (int i = 1, cnt = 0; i <= n; ++i) {
    ++cnt;
    if (cnt >= a[i]) {
      ++res;
      cnt = 0;
    }
  }
  cout << res << endl;
}

signed main() {
  ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
  int T = 1;
  cin >> T;
  for (int t = 1; t <= T; ++t) {
    solve();
  }
  return 0;
}

C. Count Triangles

先讲一下我的思路。

A≤x≤B≤y≤C≤z≤D。

因为 x 范围不大，考虑枚举 x 的值。这样对于任意满足要求的 y，都有 $C\le z\le \min(D,x+y-1)$，或者说，z 的方案数为 $\max(0,\min(D,x+y-1)-C+1)$。令这个东西为 $f(y)=\max(0,\min(D,x+y-1)-C+1)$，函数图像大概长这样。

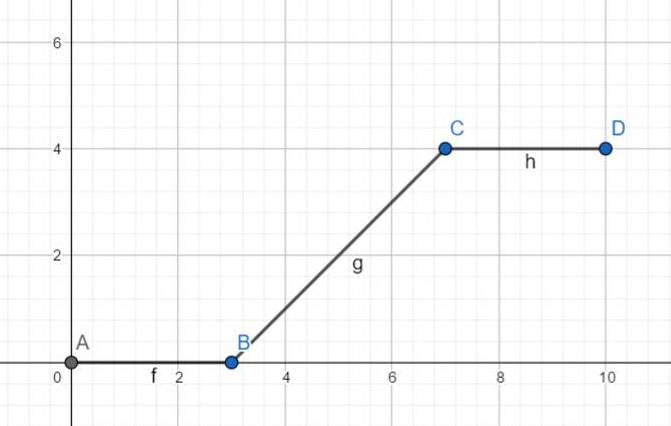
先一次函数上升，然后变成常函数。此时就能成两段讨论（一次函数和常函数），求出两个转折点什么的，太过于数学，逃了。

然后放个没人能看懂的代码（经刘老师提醒，2020-5-17 11:45 之前放的是错误代码，现已更正）。

#include <bits/stdc++.h>
using namespace std;
#define repeat(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define repeat_back(i,a,b) for(int i=(b)-1,_=(a);i>=_;i--)
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
const int N=200010; typedef long long ll;
#define int ll
int a,b,c,d;
signed main(){
    cin>>a>>b>>c>>d;
    int ans=0;
    repeat(i,a,b+1){
        int x=max(c,i+b-1); //第一个转折点
        int y=min(i+c-1,d); //第二个转折点
        int l=x-c+1,r=y-c+1;
        if(x<=y)ans+=(l+r)*(r-l+1)/2; //一次函数（等差数列求和）
        if(i+c-1>max(x-1,y))ans+=(i+c-1-max(x-1,y))*(d-c+1); //常函数
    }
    cout<<ans<<endl;
    return 0;
}

等会补个别人家的代码（雾，我作业来不及了，不补了）。

D. Game With Array

这题就一 sb 题。如果 $2N> S$，这意味着序列中至少存在一个 1，然后。。就 NO 了（还没证明）。

如果 $2N\le S$，那就构造一个序列：[2,2,2,...,2,(S-2(N-1))]，所有数都大于等于 $2$，所以这个序列的任意子序列之和都不可能是 $1$，也不可能是 $S-1$（因为存在子序列和为 $S-1$ 就必然存在子序列和为 $1$）。而子串又是一种特殊的子序列，所以完全 ojbk。

更：看了一下官方题解，来证明一波 $2N>S$ 的情况。

先假定 $K\le \dfrac S 2$。对序列求个前缀和 $sum[i]=\sum\limits_{j=1}^{i}a[j]$，$sum[0]=0$。我们知道区间和相当于两个前缀和的差值，而这个差值不能等于 $K$ 或者 $S-K$，这意味着对于每个 $sum[i]$ 都不能出现另一个 $sum[j]=(sum[i]+K)\%S$（非常巧妙，如果 $sum[i]+K\ge S$，取模后正好等于 $sum[i]-(S-K)$，差值为 $S-K$，太牛逼了）。

也就是，对每个 $sum[i]$，我们认为它占用了两个位置 $sum[i]$ 和 $(sum[i]+K)\%S$。总共 $S$ 个座位，要坐 $2N$ 个人，还有 $2N>S$ 的限制，想想都不可能。

#include <bits/stdc++.h>
using namespace std;
#define repeat(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define repeat_back(i,a,b) for(int i=(b)-1,_=(a);i>=_;i--)
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
const int N=200010; typedef long long ll;
#define int ll
int n,s;
signed main(){
    cin>>n>>s;
    if(2*n<=s){
        cout<<"YES"<<endl;
        repeat(i,0,n-1)cout<<2<<' ';
        cout<<s-(n-1)*2<<endl;
        cout<<1<<endl;
    }
    else
        cout<<"NO"<<endl;
    return 0;
}

E. Restorer Distance

我们可以很轻松地算出，如果最终状态为每个位置高度为 $H$ 的代价是多少。因此 $H$ 的选取就成为本题的关键。

大佬们就能一眼看出，代价对 $H$ 存在单峰（随 $H$ 先递减后递增），因此三分。那么为什么存在单峰呢？太难顶了，留作习题答案略（qwq）。

我的三分其实就是二分，感觉能加一点速（？）感觉最快的可能是 1.618 优选法，但是我写不来（？）。

我的方法是 $O(n\log n)$，标程是 $(\log^2n)$ 因为处理了前缀和，get_cost() 里只要 lowerbound 一下就能算答案了，真是妙啊。

#include <bits/stdc++.h>
using namespace std;
#define repeat(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define repeat_back(i,a,b) for(int i=(b)-1,_=(a);i>=_;i--)
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
const int N=100010; typedef long long ll;
#define int ll
int n,A,B,C;
int a[N];
int get_cost(int h){
    int up=0,down=0;
    repeat(i,0,n)
        (h>a[i]?up:down)+=abs(a[i]-h);
    int t=min(up,down);
    return (up-t)*A+t*B+(down-t)*C;
}
signed main(){
    cin>>n>>A>>C>>B; B=min(B,A+C);
    repeat(i,0,n)
        cin>>a[i];
    int l=0,r=1e9+1;
    while(l<r){
        int x=(l+r)/2,y=x+1;
        if(get_cost(x)<get_cost(y))r=y-1;
        else l=x+1;
    }
    cout<<get_cost(l)<<endl;
    return 0;
}