Axiomofchoice's Blog
Axiomofchoice
2021-01-29
目录

Codeforces Round 698 (Div. 2) 题解 全部6题

div2 传送门 (opens new window)

div1 传送门 (opens new window)

# A. Nezzar and Colorful Balls

大意：给一个单调不减序列，要给每个数染色使得同一种颜色组成的序列单调上升，求染色数最小值。

因为对一种颜色 color_i 来说，每种数字只能有一个数字染 color_i 颜色（比如很多个 "2" 中只能有 1 个 "2" 染成红色），所以有多少个相同的数字就对应需要多少种颜色，答案自然是出现频次最多的数字的个数。

#include <bits/stdc++.h>
using namespace std;
const int N=200010; typedef long long ll;
signed main(){
    int T; scanf("%d",&T);
    while(T--){
        int n; scanf("%d",&n);
        int pre=-1,now=0,ans=0; // pre是前
        for(int i=0;i<n;i++){
            int x; scanf("%d",&x); // x
            if(pre==x)now++; else now=1,pre=x;
            ans=max(ans,now);
        }
        printf("%d\n",ans);
    }
    return 0;
}

# B. Nezzar and Lucky Number

大意：判断一个数是否能被表示为若干（十进制表示下）含有数码 d 的数字之和。

我的代码太生草了（。

首先可以猜到，很大的数字可以转换成 \overline{dX} 和 d 的组合。比如 d=7 时，取一个 \ge 70 的数 n，由于 70,71,...,76 构成了模 7 的剩余系（说人话：n 一定与 70,71,...,76 其中一个数同余），我们就可以将 n 表示为 \overline{7M}+\tfrac{n-\overline{7M}}7\times 7（M=n\bmod 7，可以证明 \tfrac{n-\overline{7M}}7 一定是个非负整数）。

这样，我们只要考虑 n<d\times10 的情况了。为了节省时间，当然是怎么简单怎么来了，直接上暴力（我写的记忆化搜索，不清楚不记忆化行不行）。

#include <bits/stdc++.h>
using namespace std;
const int N=200010; typedef long long ll;
int ans[10][100];
bool calc(int d,int n){
    if(n>=d*10)return 1;
    if(n<d)return 0;
    if(n%10==d)return 1;
    if(ans[d][n]!=-1)return ans[d][n];
    return ans[d][n]=
        calc(d,n-d) ||
        calc(d,n-10-d) ||
        calc(d,n-20-d) ||
        calc(d,n-30-d) ||
        calc(d,n-40-d) ||
        calc(d,n-50-d) ||
        calc(d,n-60-d) ||
        calc(d,n-70-d) ||
        calc(d,n-80-d) ||
        calc(d,n-90-d);
}
signed main(){
    memset(ans,-1,sizeof ans);
    int T; scanf("%d",&T);
    while(T--){
        int d,q; scanf("%d%d",&q,&d);
        while(q--){
            int n; scanf("%d",&n);
            puts(calc(d,n)?"YES":"NO");
        }
    }
    return 0;
}

# C. Nezzar and Symmetric Array

大意：a 是一个长度 2n、对称的、数字互不相同的数列，对称意味这每个数都能找到对应的相反数。d_i=\sum_{j=1}^{2n}|a_i-a_j|，已知数列 d 问是否存在数列 a。

先对 d_i 排个序。

如果原数列 a 是 4 个数 A,-A,B,-B，0<A<B，那么 A 对应的 d 值是 2A+2B，B 对应的 d 值是 4B。这样我们大致得知一个结论，一个数的 d 值就是有多少个数绝对值比它小 * 它的绝对值 + 剩下的数绝对值之和。

根据上述结论，我们又可以得到三个推论，a_i=-a_j\Rightarrow d_i=d_j（或者说 d_i 是两个两个出现的），d_i 是偶数，任意 4 个 d_i 不相等（因为数列 a 互不相等）。

如果上面都成立，我们就可以把长度为 2n 的 d_i 简化成长度为 n 的数列 e_i=\dfrac 1 2 d_{2i}，那么 a_i 也可以去掉那些负数的部分留下正数的部分。

（e_i 为有多少个数比 a_i 小 * a_i + 剩下的数之和，其中 a_i 已经去掉负数了）。

然后我们发现，e_n 其实就是 n 倍 a_n，而 e_{n-1}-a_n 其实就是 n-1 倍 a_{n-1}，e_{n-2}-a_n-a_{n-1} 其实就是 n-2 倍 a_{n-2}，依次类推，我们可以计算出所有 a_i。

#include <bits/stdc++.h>
using namespace std;
const int N=200010; typedef long long ll;
ll a[N],d[N],e[N];
#define GG {puts("NO"); return;}
void solve(){
    int n; scanf("%d",&n);
    for(int i=1;i<=n*2;i++)
        scanf("%lld",d+i);
    sort(d+1,d+n*2+1);
    for(int i=1;i<=n*2;i++){
        if(d[i]%2!=0)GG;
        if(i%2==1){
            if(d[i]!=d[i+1])GG;
            if(i!=1 && d[i]==d[i-2])GG;
        }
    }
    for(int i=1;i<=n;i++)e[i]=d[i*2]/2;
    ll sum=0;
    for(int i=n;i>=1;i--){
        if((e[i]-sum)%i!=0)GG;
        a[i]=(e[i]-sum)/i;
        sum+=a[i];
    }
    if(a[1]<=0)GG;
    puts("YES");
}
signed main(){
    int T; scanf("%d",&T);
    while(T--)
        solve();
    return 0;
}

# D. Nezzar and Board

大意：初始黑板上有 n 个数，你可以从中取两个数 x,y 并把 2x-y 写在黑板上。问给定数字 k 是否能被写在黑板上。

从几何（？）的角度思考，（或者瞎*b试一试就可以看出）2x-y 其实就是 y 关于 x 对称的点。

假设一开始只有两个数 x,y，不断对称对称，就会出现相邻间隔为 |x-y| 的很多数。或者说，(n-x) \equiv 0 \pmod {|x-y|} 的任意整数 n 都能被表示出来了。

如果一开始有三个数 x,y,z，会发生什么呢？根据欧几里得算法，（哦细节就不说了，总之就是——）会出现间隔为 \gcd(|x-y|,|x-z|) 的很多数。这样，三个数 x,y,z 可以简化成两个数 x,x+\gcd(|x-y|,|x-z|)，不断这么操作，再多的数也都只剩两个数了。

以上仅考虑数字之间互不相同的情况，相同情况要特殊处理。

//#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
#define repeat(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define repeat_back(i,a,b) for(int i=(b)-1,_=(a);i>=_;i--)
#define mst(a,x) memset(a,x,sizeof(a))
#define fi first
#define se second
mt19937 rnd(chrono::high_resolution_clock::now().time_since_epoch().count());
//int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
const int N=200010; typedef long long ll; const int inf=~0u>>2; const ll INF=~0ull>>2; ll read(){ll x; if(scanf("%lld",&x)!=1)exit(0); return x;} typedef double lf; const lf pi=acos(-1.0); lf readf(){lf x; if(scanf("%lf",&x)!=1)exit(0); return x;} typedef pair<ll,ll> pii; template<typename T> void operator<<(vector<T> &a,T b){a.push_back(b);}
const ll mod=(1?1000000007:998244353); ll mul(ll a,ll b,ll m=mod){return a*b%m;} ll qpow(ll a,ll b,ll m=mod){ll ans=1; for(;b;a=mul(a,a,m),b>>=1)if(b&1)ans=mul(ans,a,m); return ans;}
#define int ll
int a[N];
void Solve(){
    int n=read(),k=read();
    repeat(i,0,n){
        a[i]=read();
    }
    int d=-1;
    sort(a,a+n);
    repeat(i,0,n-1)
    if(a[i]!=a[i+1]){
        if(d!=-1)d=__gcd(d,a[i+1]-a[i]);
        else d=a[i+1]-a[i];
    }
    if(d==-1){
        puts(k==a[0]?"YES":"NO");
    }
    else{
        puts((k-a[0])%d==0?"YES":"NO");
    }
}
signed main(){
    //freopen("data.txt","r",stdin);
    int T=1; T=read();
    repeat(ca,1,T+1){
        Solve();
    }
    return 0;
}

# E. Nezzar and Binary String

大意：给 01 字符串 s,f，初始字符串为 s，每次断言区间 [l_i,r_i] 都是 0 或都是 1，然后修改这个区间的 x 个字符，x 严格小于区间长度的一半，最后断言字符串=f。问是否可以让所有断言都成立。

考虑倒着操作，即从 f 出发，先修改区间再断言。这样的操作就是唯一的，即修改区间内出现次数少的所有字符。

维护区间赋值和区间求和考虑用线段树。

//#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
#define repeat(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define repeat_back(i,a,b) for(int i=(b)-1,_=(a);i>=_;i--)
#define mst(a,x) memset(a,x,sizeof(a))
#define fi first
#define se second
mt19937 rnd(chrono::high_resolution_clock::now().time_since_epoch().count());
//int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
const int N=200010; typedef long long ll; const int inf=~0u>>2; const ll INF=~0ull>>2; ll read(){ll x; if(scanf("%lld",&x)!=1)exit(0); return x;} typedef double lf; const lf pi=acos(-1.0); lf readf(){lf x; if(scanf("%lf",&x)!=1)exit(0); return x;} typedef pair<ll,ll> pii; template<typename T> void operator<<(vector<T> &a,T b){a.push_back(b);}
const ll mod=(1?1000000007:998244353); ll mul(ll a,ll b,ll m=mod){return a*b%m;} ll qpow(ll a,ll b,ll m=mod){ll ans=1; for(;b;a=mul(a,a,m),b>>=1)if(b&1)ans=mul(ans,a,m); return ans;}
// #define int ll
int in[N]; 
struct seg{
    #define U(x,y) (x+y)
    #define a0 0
    void toz(ll x){z=x,state=1;}
    void toa(){a=z*(r-l+1),z=0,state=0;}
    ll a,z; bool state;
    int l,r; seg *lc,*rc;
    void init(int,int);
    void up(){a=U(lc->a,rc->a);}
    void down(){
        if(!state)return;
        if(l<r){lc->toz(z); rc->toz(z);}
        toa();
    }
    void update(int x,int y,ll k){
        if(x>r || y<l){down(); return;}
        if(x<=l && y>=r){toz(k); down(); return;}
        down();
        lc->update(x,y,k);
        rc->update(x,y,k);
        up();
    }
    ll query(int x,int y){
        if(x>r || y<l)return a0;
        down();
        if(x<=l && y>=r)return a;
        return U(lc->query(x,y),rc->query(x,y));
    }
}tr[N*2],*pl;
void seg::init(int _l,int _r){
    l=_l,r=_r; state=0; z=0;
    if(l==r){a=in[l]; return;}
    int m=(l+r)>>1;
    lc=++pl; lc->init(l,m);
    rc=++pl; rc->init(m+1,r);
    up();
}
void init(int l,int r){
    pl=tr; tr->init(l,r);
}
// 以上为线段树板子
char s1[N],s2[N];
pii op[N];
void Solve(){
    int n=read(),q=read();
    scanf("%s%s",s1,s2);
    repeat(i,0,n)
        in[i]=s2[i]=='1';
    repeat(i,0,q)op[i]={read()-1,read()-1};
    init(0,n-1);
    repeat_back(i,0,q){
        int l=op[i].fi,r=op[i].se,len=r-l+1;
        int cnt=tr->query(l,r);
        if(len%2==0 && cnt==len/2){
            puts("NO");
            return;
        }
        tr->update(l,r,cnt>len/2);
    }
    repeat(i,0,n)
    if(tr->query(i,i)!=(s1[i]=='1')){
        puts("NO");
        return;
    }
    puts("YES");
}
signed main(){
    //freopen("data.txt","r",stdin);
    int T=1; T=read();
    repeat(ca,1,T+1){
        Solve();
    }
    return 0;
}

# F. Nezzar and Nice Beatmap

大意：平面 n 个点，求连接这 n 个点的路径（折线）使得形成的所有夹角小于 90 度。

一看到范围 5000，立刻往 O(n^2) 方向考虑。很快啊，发现如果连了 AB，那么过 B 做垂线后，平面被垂线分成两个半平面，下一个要连的点必须要在包含 A 的半平面中。

img

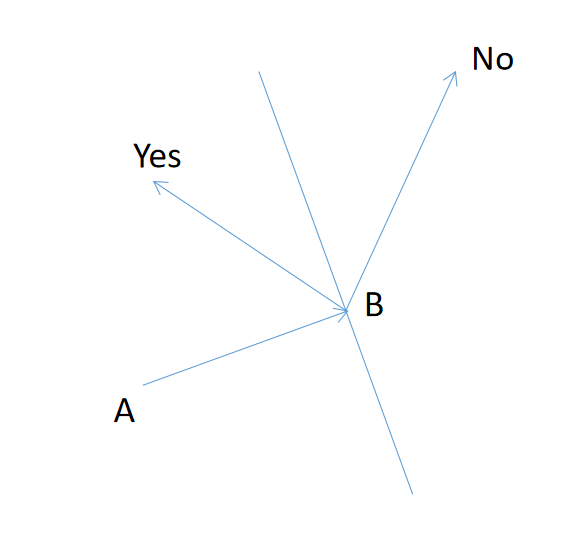
如果所有点都在这个 Yes 的半平面中就完美了。还真的可以这样，我们只要让 B 为距离 A 最远的点即可（连过的点都删了）。

问题解决。

//#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
#define repeat(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define repeat_back(i,a,b) for(int i=(b)-1,_=(a);i>=_;i--)
#define mst(a,x) memset(a,x,sizeof(a))
#define fi first
#define se second
mt19937 rnd(chrono::high_resolution_clock::now().time_since_epoch().count());
//int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
const int N=200010; typedef long long ll; const int inf=~0u>>2; const ll INF=~0ull>>2; ll read(){ll x; if(scanf("%lld",&x)!=1)exit(0); return x;} typedef double lf; const lf pi=acos(-1.0); lf readf(){lf x; if(scanf("%lf",&x)!=1)exit(0); return x;} typedef pair<ll,ll> pii; template<typename T> void operator<<(vector<T> &a,T b){a.push_back(b);}
const ll mod=(1?1000000007:998244353); ll mul(ll a,ll b,ll m=mod){return a*b%m;} ll qpow(ll a,ll b,ll m=mod){ll ans=1; for(;b;a=mul(a,a,m),b>>=1)if(b&1)ans=mul(ans,a,m); return ans;}
#define int ll
struct vec{
    int x,y; vec(){} vec(int x,int y):x(x),y(y){}
    vec operator-(const vec &b){return vec(x-b.x,y-b.y);}
    vec operator+(const vec &b){return vec(x+b.x,y+b.y);}
    void operator+=(const vec &b){x+=b.x,y+=b.y;}
    void operator-=(const vec &b){x-=b.x,y-=b.y;}
    vec operator*(lf k){return vec(k*x,k*y);}
    bool operator==

← Codeforces Round 701 (Div. 2) 题解 (ABCD)→

Theme by Vdoing | Copyright © 2021-2026 Axiomofchoice | MIT License