1. 从双指针开始讲起

说到合并 (merge) 两个有序数组，最简单强大的做法就是双指针。两个指针指向两个数组的开始位置，不断把较小元素放到 buffer 数组，对应指针向后移动。最后把 buffer 里的元素移动回原数组。

这个过程如下图所示：

这个算法在 C++ std::merge (opens new window) 里亦有记载。

---

但是这个算法需要一个 $O(n)$ 的额外空间复杂度（就是 buffer 数组），有没有办法可以原地进行呢？有的兄弟，原地算法有很多小巧思，这篇文章也算是个开头。

“原地”其实有三种含义，一是算法的结果直接写回原数组，比如 C++ std::inplace_merge 就是这个含义；二是 $O(1)$ 的额外空间复杂度；三是无额外缓冲区，这篇文章的“原地”都是这个含义。

2. rotate 区间旋转算法

原地算法基本绕不开 rotate（区间旋转），把两个相邻区间 [A B] 原地变成 [B A]，保持区间内部顺序不变。这个方法不唯一，最经典的做法是三次翻转法（或手摇算法）：先分别翻转区间 A 和区间 B，再整体翻转整个区间 [A B]，就能得到 [B A]。

这个过程如下图所示：

这个算法在 C++ std::rotate (opens new window) 里亦有记载。

3. inplace merge 的分治算法

（我们约定 merge 的接口是，输入一个长度为 n 的数组 arr 和一个位置 pos，arr[0] ... arr[pos - 1] 属于第一个有序数组 A，arr[pos] ... arr[n - 1] 属于有序数组 B，merge 的结果是合并两个有序数组为 arr[0] ... arr[n]）

怎么做呢？答案是简化的快速排序。

我们选数组中的一个数 pivot = arr[x]（马上讲怎么选这个数）。由于两个数组一开始是有序的，每个数组天然划分成小于 pivot、大于等于 pivot 两个区间，一共 4 个区间。只要把中间两个区间旋转一下，这时候变成了左边两个有序数组，右边也是两个有序数组，递归即可。

那么怎么选择 pivot 呢？可以选择中位数，我们模拟双指针的方法可以把中位数求出来，但是这样会有找中位数的开销。所以更合理的做法是取两个有序数组里较长的那个的中间值，另一个数组就用二分查找来划分。这样最坏情况也能 1:3 的比例划分数组，整个算法时间复杂度 $O(n \log n)$，读者自证不难。因为需要调用栈，额外空间复杂度 $O(\log n)$。

---

我们来看一个例子，初始数组 [2, 5, 6, 7, 12, 19], [1, 4, 6, 7, 8, 11, 13, 14, 14, 18]：

---

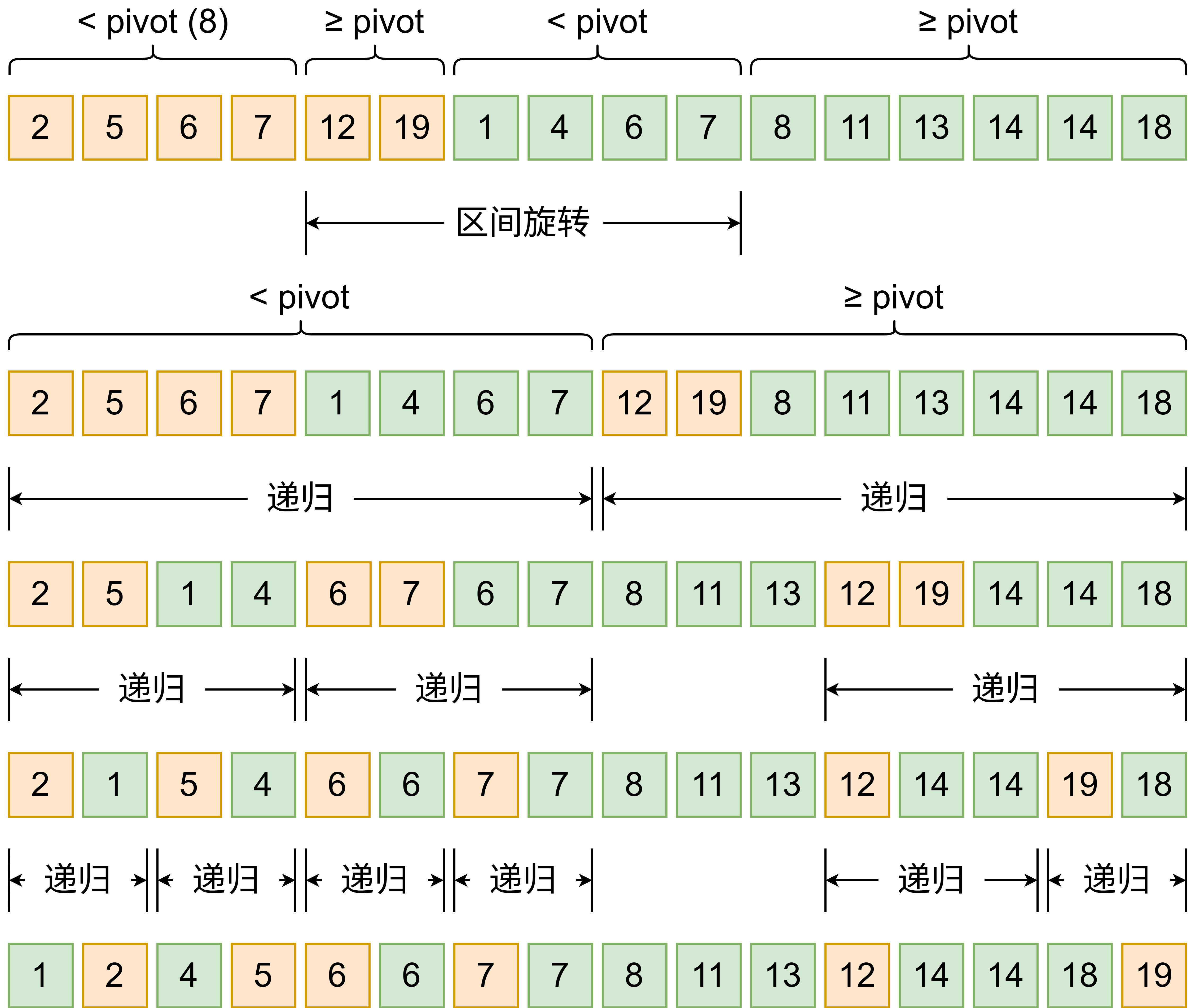
这个算法在 C++ std::inplace_merge (opens new window) 里亦有记载（如果空间不够的话）。

我们顺便浏览一下 libstdc++ 的实现。

1. std::inplace_merge (opens new window) 会直接调用 std::__inplace_merge。
2. std::__inplace_merge (opens new window) 如果申请 buffer 失败，调用 std::__merge_without_buffer。
3. std::__merge_without_buffer (opens new window) 这里就是上面算法的实现了。

4. stable partition 的分治算法

划分 (partition) 是快速排序里的一个步骤，就是给定一个数字 pivot，把数组里小于 pivot 的放前面，大于等于 pivot 的放后面。这里再加个稳定的要求，就是保持小于 pivot 的数字之间顺序不变，大于等于同理。

怎么做呢？答案是简化的归并排序。

我们取中间位置，左右两边分别递归求解，这样左右分别得到小于 pivot、大于等于 pivot 的两个区间，一共 4 个区间。这时候只要把中间两个区间旋转一下，就结束了。旋转 $O(n)$ 就行了，整个算法时间复杂度 $O(n \log n)$，读者自证不难。

这个算法在 C++ std::stable_partition (opens new window) 里亦有记载（如果空间不够的话）。

5. 从 merge 到 partition

有没有发现，我讲 stable partition 算法时好像在倒着讲述 inplace merge 算法。

merge 和 partition 仿佛就是关于时间对称的两个算法。它们甚至你中有我，我中有你：inplace merge 是简化的快速排序，单个步骤是 partition；stable partition 是简化的归并排序，单个步骤是 merge。

非常神奇。

---

相比有人不满意 $O(n\log n)$ 的时间复杂度吧。其实存在 $O(n)$ 的原地稳定 merge 算法，这个算法也能很容易实现 $O(n \log n)$ 原地稳定排序，这边就挖个坑。